Figure 51: here's the trig thing

by Russ Elliott

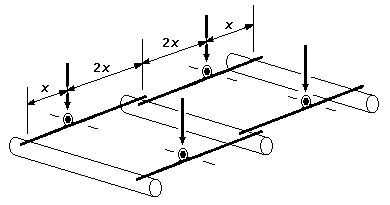Figure 51 Three-axle quadruple springy equalising beam arrangement

For suspending three axles, figure 51 of Digest 41.0 is a useful arrangement, first advocated to my knowledge by Keith Norgrove. With the pivot/fulcrum points of each of the four beams at one-third of the distance from the outer axle to the centre axle, the centre axle ends of each beam provide half the downward force as that on their outer axle, in accordance with the principle of moments, but since the inner ends of each beam impinge together on the centre axle, all axles will end up equally loaded if the centre of gravity is at the midpoint of the wheelbase.

A typical application of figure 51 would be on bogies or tenders where the frame length precludes incorporating a CSB over all the axles. The purpose of this page is to describe a subtle implementation issue concerning the vertical positioning of the fulcrum/pivoting point of each beam.

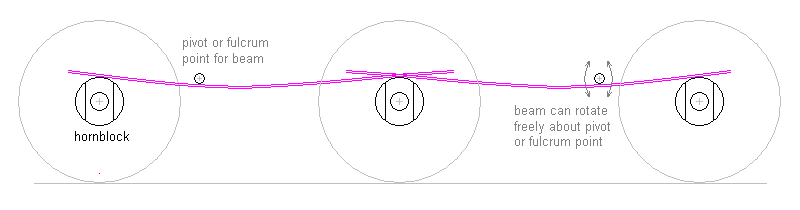
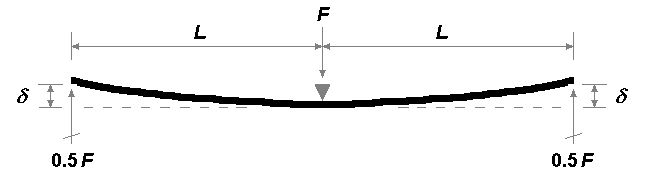
With symmetric springy equalisers with arms of equal length, the deflections δ and the reaction forces at each end will be the same. Such a springy equaliser is in effect two simple cantilevers joined on a common axis. The datum bending plane is horizontal, and the deflection distance is from the underside of the spring to that bending plane.

With the asymmetric arrangement however of figure 51, although we want only half the downforce at the end of the longer arm, the deflection at that end will be 4δ, because the deflection is proportional to the cube of the cantilever length:

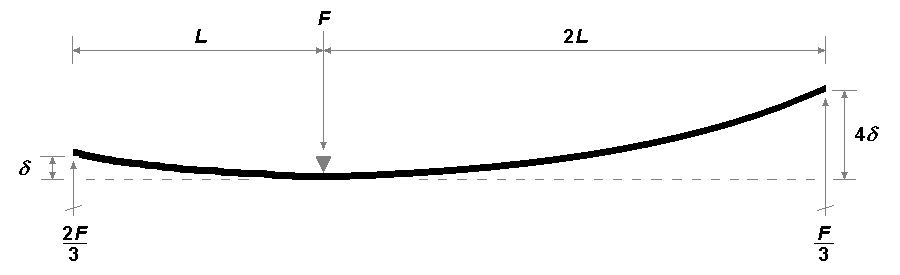
In the above diagram, the datum bending plane is still horizontal, but this is not what we want for a figure 51 implementation: what we want is for the deflection heights to be on the same horizontal, thus we have to rotate the above diagram (about point O) to achieve this:

To determine the vertical distance between points O and D and the relationship of that distance to the design deflection distance δ, we can represent the above diagram in trigonometry:

The rotation of the datum bending plane is small (approximately 5°), so OB can be taken as equal to δ. OFGB is a parallelogram, therefore OB = CD = FG = δ, and EF is therefore 3δ. Triangles OEF and OAC are similar, therefore AC = δ. The vertical distance between O and D is therefore AC + CD = 2δ, or in other words:

δ ' = 2δ

first issued 9 May 2012