Questions relating to the choice of deflection value in coil springs and springy beams

by Russ Elliott
" The mathematics are solid and stable - it's our inadequate perception that's confusing the issue."    
Click here for worked examples of beam deflection values


Spring characteristics: resumé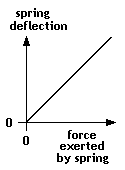

force v deflection characteristic of spring
Within its elastic limit, the deflection δ  of a spring, whether as a coil or as a beam, is linearly proportional (but see the caveat below on the use of small compression springs) to the force F applied to or by that spring. This principle applies even to non-prismatic beams. (A non-prismatic beam is a beam with a varying cross-section, or where different moments of inertia are present.)

The relationship between deflection and force is known as the stiffness, or springrate, k, of the spring:

     k =  F / δ

i.e. the greater the springrate, the less the deflection for a given force F. High springrate springs are 'hard'. Low springrate springs are 'soft'.

For beam springs, k is based on the length, material and cross-sectional shape of the beam, as described in the beam deflection article. For coil springs, see the diagram below.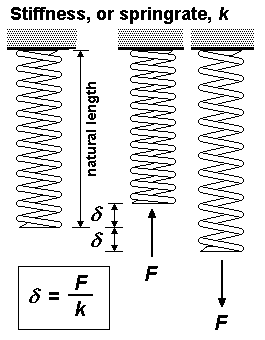

stiffness, or springrate, of a coil spring

Introduction

There is little evidence to support the recommendation that the value for hornblock deflection under the weight of a 4mm scale locomotive should be 0.5mm. The source of the 0.5mm is the 'Hal o the Wynd' article by Chris Pendlenton in Model Railway Journal issue Nos 28 and 29, which describes the fitting and operation of leaf springs to a Pacific loco.

More fundamentally, the purpose of the beam deflection article is questioned: what are we trying to achieve?

The question of the choice of spring deflection value cannot be divorced from the state of the track. If you have perfectly level track, there will be no need, in the absence of other forces, for any springing of wheelsets.

Even where track is not level, the choice of a design spring deflection value cannot be divorced from the length of the loco or vehicle wheelbase in question.

For wagons and coaches, with the exception of coupling and buffing forces, the only force acting on the springs is the distributed weight of the vehicle. When track irregularities are encountered, the springs need to act with a force sufficient to keep the wheels in reasonable contact with the rails such as to not risk derailment. They do not need to exert a strong force throughout the whole deflection distance: the unequal shifting of loads applied by each wheel will not be particularly critical. Providing a good dynamic balance can be achieved amongst the springs, they can therefore be set softer than would be the case for locos. Bogie vehicles have inherently good longitudinal balance, and the undesirable dynamic instability that low springrates can give rise to is therefore minimised. It is likely though that the bogies on a bogie vehicle will be mounted such that they do provide compensation for gross and deliberate departures from the level track datum, as would be encountered in track cant and at changes in gradient.

Coupling and buffing forces can be significant, particularly the latter when vehicles are being pushed and where buffers of adjacent vehicles are not in good alignment with each other.

For locos, the situation is not so easy to assess.

There is some evidence to show that prototype loco springs were set to deflect in the order of 0.16" to 0.17" per ton of wheel weight: typically, this would produce about 1.5" total deflection (0.5mm in 4mm scale). Any further prototype evidence on this matter is welcomed.

For locos, a compromise has to be achieved. We want any deflection of a spring to continue to exert a strong force downward on the wheel. If we assume a track irregularity of '0.5mm', then a soft spring would seem to be appropriate if we want the wheel to maintain somewhere near its undeflected traction value. (A 0.25mm track defect, for example, would mean that an individual wheel could lose half its loading.) Against this, soft springs will make the loco ride height difficult to set and maintain, and can instigate undesirable amounts of roll and pitch arising from the effects of drawbar pull and the effects of inaccuracies in wheels and rod and crankpin settings. Also, a long wheelbase loco will need to cope with all the track irregularities it is expected to have over its wheelbase, and therefore needs to be assessed somewhat differently to locos with a short wheelbase.


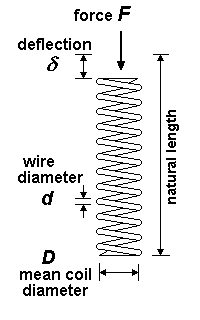
deflection of a coil spring

Coil spring deflection

Unlike a beam, the wire of a coil spring bends primarily in torsion. The deflection of a coil spring is:

   δ = 8NaFD3/Gd4

where Na is the number of 'active' coils (usually one or two less than the full number of coils, depending on how the coil spring wire is terminated at the ends of the coil), and G  is the Modulus of Rigidity of the wire material (G is 75 to 80 GPa for spring steel).

Comparison of beam and coil springrates

A coil is not necessarily 'softer' than a beam. Compare the springrates for a centre-loaded beam and a coil:

   kbeam = 3Eπd4/4L3
   kcoil = Gd4/8NaD3

Taking typical values for E and G for spring steel, and taking a (hypothetical) example of where the length L of a beam spring is made the same as the length of the wire in a coil spring (approximately πNaD), the ratio of these springrates (kbeam / kcoil) is approximately equal to:

  (1.6/Na2) x (dbeam / dcoil)4

This expression is of little practical use, but indicates that the key variables are the number of active coils in a coil spring and the differences in diameters of the wire used in the two types of spring. If example values of a 15 thou loco driver beam spring and a 5-turn coil spring of say 4 or 5 thou wire are used, we can see that the beam spring is harder than the coil for these values. Other values will give very different results. Coil springs can be made just as 'hard' as beam springs.


Useful springrates for driving wheels

In 4mm scale, the scale weighting factor is usually between 4g and 6g per prototype ton. Taking typical prototypical driver weights of between 14 and 20 tons, and using the notional 0.5mm desired deflection value, approximate 4mm scale model springrates are derived, assuming 2 hornblocks per axle.

8- and 10-coupled locos have inherently better pitch stability compared to 4- and 6-coupled locos, and thus springrates slightly lower than those indicated could be entertained for the larger locos.
Approximate springrate per hornblock
Scale
weighting
factor
Prototype axle weighting
14 ton
20 ton
4g/ton 0.55N/mm 0.8N/mm
6g/ton 0.8N/mm 1.2N/mm



Caveats on the use of small compression coil springs

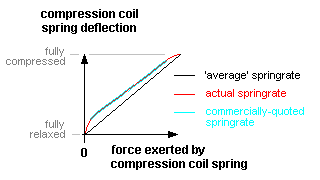
deflection characteristic of a small compression coil spring
Springrates for short length coil compression springs are somewhat problematic. Owing to end-coil effects, and depending on how the coils are terminated, the springrate over the initial part of the compression tends to be considerably lower than an 'average' value determined over the whole of the distance between the fully relaxed and the fully compressed states, and the springrate over the final part of the compression tends to be considerably higher than that average value. Commercially-quoted springrates are usually derived from the central 60% of the deflection range. The graph shows an exaggerated representation of this characteristic.

If the linear proportion of the spring characteristic is to be used, our desired 0.5mm deflection value indicates an optimum relaxed coil spring length of less than 4mm. Commercial compression coil springs of this order of length are inevitably subject to some variation in manufactured relaxed length, and thus, for a set of springs in a chassis, the consistency and accuracy of their spring characteristics over such a small deflection window is uncertain.

It is this unpredictability of the short travel distance of small coil springs that make beam springs a more attractive proposition: beam spring deflection is predictable and controllable.


Pony truck springing

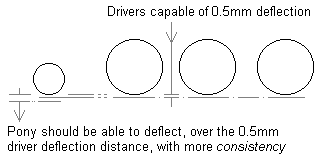
There are good reasons why the '0.5mm' deflection should not be applied to a pony truck:
  • such a deflection would require the pony truck axle datum height to be engineered very tightly with respect to the datum height of the driver axles;

  • the pony truck is required to act only with a down force sufficient for consistent and reliable track-holding.
 pony truck setting
A low-springrate, long-travel, springing characteristic is therefore desirable for a pony truck. To implement this notion, a distinction has to be made between a single spring acting on top of a pony truck frame on one hand, and on the other hand a pony truck where the hornblocks are individually sprung: the unsprung weights are very different.

Prototype pony truck weights, which are quoted to include their unsprung weights, tend to be in the region of 6 to 12 tons.

 
to be continued (maybe)


© Russ Elliott
July 2001, revised August 2001, May 2003, August 2003


Return to top of page
Comment on this page
Beam menu page